
La vie moderne est étroitement liée aux ordinateurs. Mais la technologie informatique classique a déjà largement atteint ses limites. Les scientifiques sont donc à la recherche de nouvelles orientations qui pourraient permettre une percée révolutionnaire dans le domaine de l’informatique. Le plus prometteur est considéré comme l’ordinateur quantique, qui devrait être beaucoup plus efficace que tout ce qui a été créé jusqu’à présent[1] .
C’est un ordinateur tellement complexe qu’il est difficile de le comprendre car il n’utilise plus le système binaire (où il y a de très longues séries de 0 et de 1 qui constituent, lancées à toute vitesse, les séquences décrivant la réalité et le mouvement) mais le système quantique, qui est tridimensionnel : si en arithmétique un plus un donne deux, alors si l’on veut faire un calcul quantique, il faut ajouter à 2 toutes les positions occupées dans l’espace par la source d’énergie qui a déclenché la question et celles d’où est venue la réponse. Donc un plus un donne un résultat différent à chaque fois. Et c’est là que les choses deviennent intéressantes, effrayantes, inquiétantes.
Parce que nous entrons dans un monde où un objet fondamental pour notre survie ne pourra plus être réparé par l’homme. Le jour où nous déciderons d’utiliser un ordinateur quantique ou de doter notre maison de la capacité de nous contrôler selon les principes de la physique quantique, nous devrons nous en remettre entièrement à l’intelligence artificielle, seule capable de comprendre et de réparer des systèmes aussi complexes. Il n’est pas nécessaire de regarder un film de science-fiction pour craindre un changement de cette ampleur.
Un nouveau type de particule dans l’univers

boson de Higgs[2]
Nous vivons dans un monde tridimensionnel où tout s’explique par les lois de la physique et où, si l’on décompose notre monde, il n’y a que deux types de particules : les « fermions », qui se repoussent, et les « bosons », qui aiment se coller les uns aux autres. De l’énergie en mouvement et de l’énergie statique, en somme. Un exemple bien connu de fermion est l’électron qui transporte l’électricité, et un exemple bien connu de boson est le photon qui transporte la lumière. Mais si l’on considère le monde bidimensionnel, où les particules ne peuvent tourner les unes autour des autres que de deux manières différentes (dans le sens des aiguilles d’une montre ou dans le sens inverse), on trouve un autre type de particules : les anions, qui ne se comportent ni comme des fermions ni comme des bosons et qui interagissent quelque part entre l’attraction et la répulsion. Leur existence a été annoncée pour la première fois à la fin des années 1970 en tant qu’hypothèse logique, mais la preuve expérimentale de leur existence n’a été obtenue qu’en 2020 .[3]
Les anions sont des particules chargées qui se forment lorsqu’un atome ou un groupe d’atomes reçoit une ou plusieurs charges négatives supplémentaires. Les atomes sont constitués de protons (chargés positivement), de neutrons (non chargés) et d’électrons (chargés négativement). Dans un atome neutre, le nombre de protons est égal au nombre d’électrons, ce qui garantit sa neutralité. Toutefois, lorsqu’un atome ou un groupe d’atomes acquiert un ou plusieurs électrons supplémentaires, il se forme des anions[4] .
L’existence des anions a été démontrée par une équipe de scientifiques français. Ils ont créé un minuscule collisionneur bidimensionnel dans lequel les particules chargées se déplacent comme un carrefour à quatre voies, avec deux entrées et deux sorties[5] . Si vous envoyez des bosons « similaires » le long de deux chemins intérieurs, ils se rencontreront au carrefour et sortiront ensemble par le même chemin. Cependant, si vous envoyez des particules chargées avec une charge négative supplémentaire, elles se comportent de manière très différente : parfois elles se rejoignent, parfois non. Bien qu’elles aient tendance à se regrouper en tant que bosons, le degré exact de proximité dépend de leur nature vibratoire, qui est la mesure qui détermine en fin de compte le calcul[6] . En d’autres termes, au lieu qu’il n’y ait qu’une seule solution possible, il y a un nombre presque infini de solutions possibles.
Les anions obéissent à une règle d’échange inhabituelle : dans un espace bidimensionnel, un échange de deux fois les mêmes particules n’est pas équivalent à un échange sans ces particules (- x – ≠ +), car la position des particules après le double échange peut être différente de la position initiale. Ce processus d’échange des mêmes particules ou de rotation d’une particule autour de l’autre est appelé « intrication ». L' »intrication » de deux anions crée un enregistrement historique de l’événement[7] , car leurs fonctions d’onde modifiées « comptent » le nombre de particules intriquées[8] .
Si l’on considère ces « quasi-particules » en termes de théorie mathématique des groupes, les anions peuvent être divisés en groupes « abéliens » et « non abéliens », en fonction des propriétés de leur comportement dans le groupe. Un groupe abélien (ou groupe commutatif[9] ) est un groupe dans lequel l’ordre des éléments dans l’opération n’a pas d’importance. Un groupe non abélien est un groupe dans lequel l’ordre des éléments dans l’opération est important. Si les anions A et B sont non abéliens, alors en général A + B ≠ B + A. En d’autres termes, il faut compter non seulement les particules elles-mêmes, mais aussi les séquences de leurs mouvements et de leurs mutations[10] . Un calcul avec un nombre insensé de variables, tel qu’il ne peut être contrôlé de manière réaliste par les humains, et dont les résultats contredisent tout ce que nous pensions savoir, et sont pourtant vrais[11] .
Classique contre quantique

Le Mur de la domination, le premier objet quantique jamais créé en laboratoire[12]
Les anions non abéliens (ou anions non abéliens) présentent un intérêt pour la physique quantique car leurs propriétés permettent des calculs quantiques basés sur l’ordre topologique. L’ordre topologique non abélien est un état souhaitable de la matière qui présente des propriétés remarquables[13] , notamment l’existence de « quasiparticules » capables de se souvenir de la séquence dans laquelle elles oscillent. Leurs enchevêtrements sont les « qubits », la base de l’ordinateur quantique[14] . Ils constituent des éléments de base prometteurs pour les ordinateurs quantiques tolérants aux pannes, car ils deviennent prévisibles après un nombre suffisant d’observations[15] . En outre, des phénomènes tels que la cohérence quantique (cohérence du mouvement des microparticules formant un système physique donné[16] ) et la dépendance quantique (phénomène de mécanique quantique[17] , dans lequel les états quantiques de deux objets ou plus semblent interdépendants même après séparation)[18] sont associés à des éléments non abéliens.
Un objet quantique est un objet dans un microcosme, et donc très petit : le microcosme est un monde d’objets si petits qu’ils ne peuvent être observés directement à l’œil nu (molécules, atomes, particules élémentaires), et il fonctionne différemment du monde auquel nous sommes habitués : un monde dans lequel la probabilité est la pierre angulaire et l’état de l’objet ne peut être clairement défini, parce que ses propres lois et règles s’y appliquent .[19]
Ainsi, les différences entre les ordinateurs conventionnels (classiques) et quantiques commencent immédiatement par des systèmes de traitement de l’information fondamentalement différents. Les ordinateurs conventionnels utilisent des chiffres binaires pour représenter et traiter l’information. Un bit est une valeur minimale d’information, qui peut avoir une valeur de 0 ou de 1. Les ordinateurs quantiques, en revanche, utilisent des bits quantiques – qubits – qui peuvent se trouver simultanément dans les états 0 et 1[20] . Cela est dû à la nature de la mécanique quantique, dans laquelle les objets peuvent exister dans tous les états possibles simultanément, ce que l’on appelle la superposition[21] .
Le principe de superposition quantique est parfaitement illustré par l’exemple classique du chat de Schrödinger. Imaginons une chambre forte fermée, à l’intérieur de laquelle se trouvent un chat ordinaire et une machine infernale protégée par lui. Dans la machine infernale, il y a très peu d’atomes radioactifs. La probabilité qu’au moins l’un d’entre eux se désintègre en une heure est égale à la probabilité qu’aucun d’entre eux ne se désintègre, soit 50:50. Autour de la matière radioactive se trouve un écran sensible aux électrons.
Si un seul atome se désintègre, un mécanisme se déclenche qui libère un gaz toxique et le chat meurt. Nous ne pouvons pas prédire avec précision si le chat est mort ou vivant. Pour cela, il faut ouvrir le coffre-fort et regarder. Et lorsqu’on le referme, le chat se superpose : il est à la fois vivant et mort[22] . Si nous ouvrons et fermons la porte plusieurs fois, nous arrivons à un point où nous avons tellement de variables toutes aussi possibles les unes que les autres que nous devenons fous. Cet exemple illustre l’un des principes du monde quantique : la capacité d’une particule quantique à se trouver simultanément dans tous les états jusqu’à ce que l’expérimentateur fasse une observation – fixation instantanée de l’état momentané.
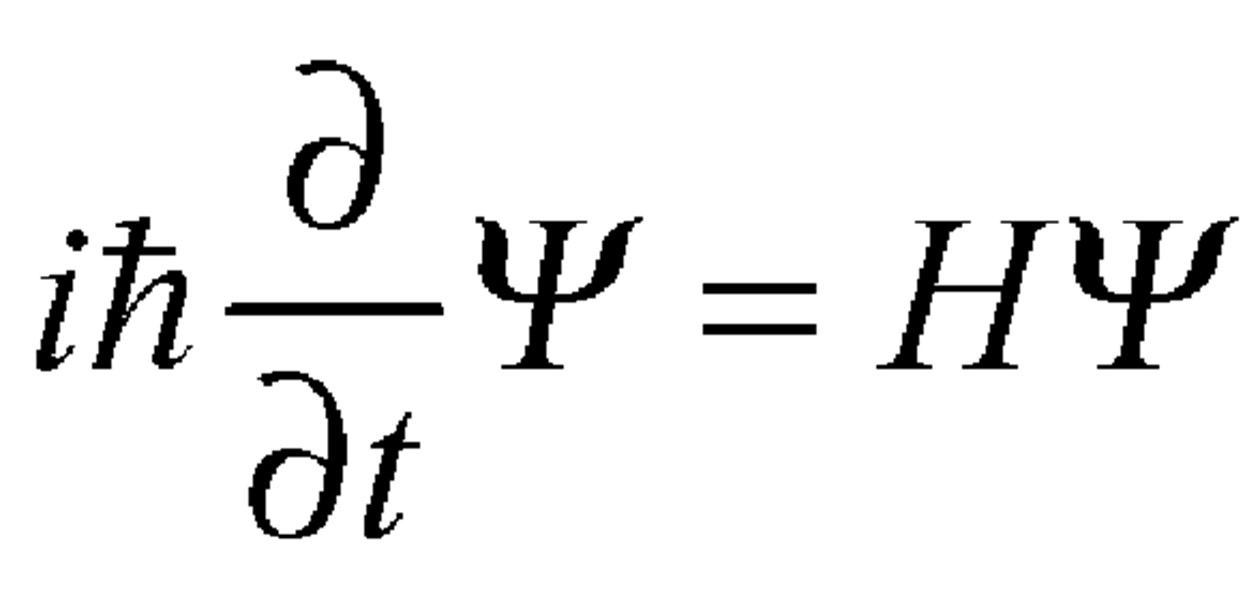
L’équation d’Erwin Schrödinger qui, en 1927, a réussi à calculer l’oscillation des particules dans l’espace, surpassant les innovations d’Einstein.[23]
Dans les ordinateurs classiques, l’information est traitée de manière séquentielle à l’aide d’actions conventionnellement simples telles que l’addition, la multiplication, les opérations logiques, etc. Les ordinateurs quantiques peuvent traiter l’information en parallèle grâce à la superposition quantique. Il ne s’agit pas d’une quantité bien définie, mais de la probabilité d’obtenir l’un de ces états. Par exemple, 3 bits d’information peuvent donner l’une des huit combinaisons de zéros et de uns : 000, 001, 010, 100, 011, 101, 110, 111. Les cubes fonctionnent avec huit combinaisons possibles en même temps, en calculant des probabilités plutôt que des valeurs explicites. Avec chaque qubit, la puissance de traitement augmente de façon exponentielle : 10 qubits peuvent opérer simultanément sur 1024 combinaisons et 30 qubits peuvent opérer sur plus d’un milliard de combinaisons[24] . Cela permet d’effectuer certaines opérations beaucoup plus rapidement.
Dans les ordinateurs classiques, l’information est traitée à l’aide de signaux électriques représentés sous forme de tension ou de courant. Les ordinateurs quantiques fonctionnent sur la base de phénomènes quantiques, qui nécessitent un équipement spécial et des contrôles environnementaux, car les particules nanométriques sont très sensibles aux influences extérieures et les états quantiques ne sont pas toujours stables.
Les ordinateurs classiques gèrent bien de nombreuses tâches, telles que le traitement de texte, l’informatique, la gestion de données, etc., tandis que les ordinateurs quantiques ont le potentiel de résoudre certaines tâches qui sont difficiles ou impossibles avec les ordinateurs classiques, telles que la factorisation de grands nombres, l’optimisation, la modélisation de systèmes complexes et la mise au point de nouveaux matériaux. Il existe de nombreux domaines prometteurs pour l’ordinateur quantique, tels que la biologie moléculaire et la génétique, les neurosciences et l’intelligence artificielle, la cryptographie et d’autres encore[25] . Partout où la probabilité l’emporte sur la clarté, l’ordinateur quantique pourrait jouer un rôle clé.
Problèmes quantiques
Illustration graphique de l’expérience du chat de Schrodinger[26]
Bien que le monde ait déjà décidé qu’un ordinateur quantique était nécessaire, la question de sa stabilité reste ouverte. La création et l’utilisation d’un état quantique topologique pourraient tout révolutionner. Les non-béleons ont une propriété unique et utile : ils se souviennent d’une partie de leur histoire. Cette « mémoire » du non-Abelion peut être représentée par une ligne droite continue dans l’espace-temps. Lorsque deux non-béleons échangent leur place, les lignes de leur mouvement se croisent. S’ils sont correctement enroulés, les nœuds et les tresses qui en résultent constituent les opérations de base d’un ordinateur quantique topologique – et c’est pourquoi ils sont si précieux : parce qu’ils accélèrent notre capacité à calculer[27] d’une manière importante.
La création d’états quantiques topologiques dépend fortement de la force des interactions entre les qubits, les unités d’information. Au fur et à mesure que des qubits sont ajoutés au système, les interactions entre eux deviennent de plus en plus complexes, ce qui rend difficile le maintien d’une protection topologique, c’est-à-dire un état dans lequel le système sera stable même en présence de perturbations externes telles que du bruit ou des défauts[28] . Mais il est difficile de créer, de manipuler et de faire des choses utiles avec des nonablions dans un ordinateur quantique. Plus il y a de variantes, plus il y a d’informations incohérentes dans le calcul global, et donc plus le niveau de complexité augmente.
Une équipe de physiciens du Quantinum, du California Institute of Technology et de l’université de Harvard a utilisé un ordinateur quantique pour créer des particules virtuelles et les déplacer de manière à ce que leurs trajectoires forment un anneau borroméen – une grille de trois cercles topologiques dans laquelle deux des trois anneaux ne sont pas connectés (c’est-à-dire que si vous retirez un anneau, les deux anneaux restants se déconnectent)[29] . Détail important : s’ils sont déconnectés, non seulement l’ordinateur ne s’éteint pas, mais il continue à chercher l’ordre dans le chaos sans relâche – il échappe tout simplement au contrôle de l’homme[30] .
Pour cette expérience, les scientifiques ont utilisé la machine la plus avancée de l’entreprise, appelée H2, équipée d’une puce capable de créer des champs électriques pour piéger 32 ions de l’élément ytterbium à sa surface. Chaque ion peut coder un cubit, une unité de calcul quantique qui peut être soit « 0 » ou « 1 », comme les bits normaux, soit une superposition des deux états simultanément. Ces ions sont enchevêtrés dans un réseau de type kagome – une mosaïque de triangles et d’hexagones réguliers s’entourant les uns les autres – et toutes les particules ont le même état quantique.
Les états intriqués, dans l’univers virtuel bidimensionnel de l’arithmétique la plus simple, ne déplacent pas d’énergie – en fait, ce sont des états dans lesquels il n’y a pas de particules en mouvement. Mais par une manipulation plus poussée, la mosaïque que nous appelons kagome peut être traduite en états excités[31] – c’est-à-dire qu’elle peut facilement être transformée en un espace dans lequel les photons, poussés par l’accélération ou la chaleur, entrent en collision et créent d’impressionnantes quantités d’énergie[32] . Cela correspond à l’apparition de particules qui doivent avoir les propriétés des particules non abéliennes (qui refusent de s’ordonner sur des pistes prédéterminées).
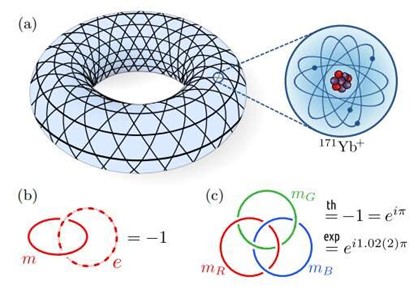
Création et gestion de fonctions d’onde non abéliennes[33]
Pour prouver que les états excités ne sont pas abéliens, les scientifiques ont effectué un certain nombre de tests. Le plus convaincant d’entre eux consiste à déplacer les états excités pour créer des anneaux de borromine virtuels[34] . L’apparence du modèle confirme le mouvement et les mesures des ions[35] . L’approche quantique présente l’avantage que, par rapport à la plupart des autres types de qubits, les ions sont piégés et peuvent être déplacés et forcés à interagir les uns avec les autres, ce qui permet aux ordinateurs quantiques d’effectuer des calculs[36] .
Cette expérience était une simulation physique d’anions non abéliens en action, qui a montré qu’ils pourraient constituer une base stable pour l’informatique quantique[37] . Les scientifiques de Google Quantum AI ont montré qu’il est possible de corriger la perte d’informations quantiques due à la perturbation du couplage des qubits qui se produit lorsqu’un système mécanique quantique interagit avec son environnement à l’aide d’anions non abéliens.
Dans la nouvelle étude, le rôle des anions non abéliens a été calculé à partir du nombre de défauts dans le code de surface (qui combine plusieurs qubits physiques en un seul code logique et est donc plus facile à concevoir) représenté sous la forme d’un graphique carré (modèle mathématique du système)[38] . Les défauts étaient de nature topologique et avaient donc les bonnes propriétés pour simplifier le graphe carré[39] . L’étude a montré qu’en déplaçant les défauts le long du graphe, il était possible de tisser et d’encoder des informations quantiques de cette manière. Les physiciens ont ainsi démontré que les qubits logiques à base de néabélions dans un processeur quantique supraconducteur sont potentiellement adaptés à l’informatique quantique[40] .
Les anions non abéliens et leurs propriétés statistiques ont une importance potentielle dans divers domaines de la science et de la technologie. Le domaine d’application le plus souhaitable de leurs propriétés uniques est l’informatique quantique, où les états quantiques topologiques des anions non abéliens peuvent créer des ordinateurs quantiques plus puissants et plus stables, capables de résoudre des problèmes complexes dépassant les capacités de leurs homologues classiques. En outre, les anions non abéliens sont théoriquement capables d’apporter des contributions importantes à la transmission, au stockage et au codage de l’information quantique.
Les néabélions sont également étudiés dans le contexte de la gravité quantique et de la théorie des cordes[41] . Leurs propriétés peuvent aider à comprendre les aspects quantiques des phénomènes gravitationnels et à trouver une unification de la physique quantique et de la théorie de la gravité[42] . Les états non abéliens sont parmi les états quantiques les plus complexes qui existent en théorie et sont prometteurs pour de nouveaux types de traitement de l’information quantique. Le fait que ces états puissent être préparés et contrôlés avec précision témoigne du développement rapide des dispositifs quantiques au cours de la dernière décennie et ouvre un certain nombre de nouvelles questions[43] .
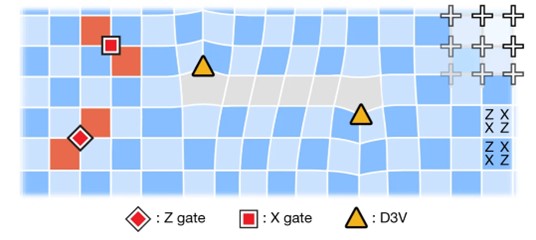
Graphique représentant le code de surface sur une grille de qubits physiques (plus). Les triangles jaunes sont les défauts responsables de la formation de la non-abélianité[44] .
Le fait que leur existence ait été prouvée représente une avancée pour la science quantique. Les néabélions pourraient devenir un outil de recherche d’états exotiques de la matière, qui sont restés jusqu’à présent une idée farfelue dans les théories des physiciens[45] . Ce sont des concepts difficiles à expliquer, mais qui affectent profondément notre système de vie : les ordinateurs classiques et même les vaisseaux spatiaux qui ont atteint la Lune et Mars fonctionnent sur la base d’un système binaire : il n’y a que des « on » et des « off » ordonnés en très longues séquences pour représenter l’ensemble du monde réel. C’est un système lent et défectueux qui, dans certaines situations, fait que l’univers, qui n’est pas binaire, se comporte comme un jeu vidéo d’il y a un demi-siècle.
La mécanique quantique tente de calculer l’univers tel qu’il est et, pour cette raison, nous devons être capables de prédire l’imprévisible, de rechercher la répétition là où il y avait des règles, des probabilités là où il y avait de la certitude. Nos ordinateurs, qu’ils soient analogiques ou numériques, contraignent le monde à la simplicité. Ce n’est pas le cas des ordinateurs quantiques. Et ce n’est pas tout : ils apprennent de manière autonome et sont capables de stocker des quantités incommensurables de données dans leur mémoire. Si vous ne frappez pas la hache, seul un ordinateur quantique peut réparer un ordinateur quantique.
L’évolution de tout cela est évidente : le quantique nous rapprochera des étoiles, mais il le fera tout seul – nous ne serons que des spectateurs, tous impliqués dans la compréhension de ce que l’ordinateur quantique a découvert, analysé, évalué, décidé, converti en connaissances utiles pour des découvertes ultérieures. Nous avons ouvert la boîte de Pandore.
[1] https://scientificrussia.ru/articles/osnova-dlia-kvantovogo-kompiutera
[2] https://www.geopop.it/cosa-sono-i-bosoni-e-quali-sono-i-principali-tipi-spiegato-in-modo-semplice/
[3] https://sciencex.com/wire-news/347971706/finally-anyons-reveal-their-exotic-quantum-properties.html
[4] https://new-science.ru/anion/
[5] Lorsqu’une particule rencontre son antiparticule, les deux s’annihilent, libérant de l’énergie pure. Après la Seconde Guerre mondiale, les scientifiques ont construit des collisionneurs, des machines qui accélèrent les protons jusqu’à ce qu’ils entrent en collision et libèrent de l’énergie. En 1960, le physicien autrichien Bruno Tuschek a eu l’idée d’utiliser des accélérateurs pour faire entrer en collision la matière et l’antimatière. Il existe aujourd’hui des exemples extrêmement complexes de collisions entre des protons et des antiprotons (qui accumulent de l’énergie). httpshttps://scienzapertutti.infn.it/7-collisorescienzapertutti.infn.it/7-collisore .
[6] https://phys.org/news/2020-04-anyon-evidence-tiny-collider.html
[7] https://phys.org/news/2020-07-evidence-anyons.html
[8] L’enchevêtrement de deux particules est une relation extraordinaire qui les lie indépendamment de toute règle évidente et qui ne peut être prédite. Dès que nous observons le mouvement des particules, nous constatons que deux ou plusieurs d’entre elles se déplacent le long des lignes de l’autre, et qu’elles sont donc intriquées. La manière dont cela est possible n’est pas claire, car les mouvements associés sont plus rapides que la vitesse de la lumière, et tout transfert d’information entre deux particules est donc impossible. Pour un observateur, plus les particules sont intriquées, plus le comportement du système est prévisible. Nous ne savons pas pourquoi, mais nous savons comment… httpshttps://www.geopop.it/una-spiegazione-semplice-dellentanglement-quantistico/www.geopop.it/una-spiegazione-semplice-dellentanglement-quantistico/ .
[9] L’arithmétique est un groupe commutatif car le résultat du calcul reste le même même si les coefficients sont inversés : par exemple, 2+1 a toujours le même résultat que 1+2 – https://www.andreaminini.org/matematica/gruppi/gruppo-abeliano.
[10] https://nplus1.ru/news/2023/05/16/non-abelian-anyons
[11] https://www.wired.it/scienza/spazio/2020/01/30/fenomeni-strambi-mondo-quantistico/ ; https://w3.lnf.infn.it/levoluzione-parallela-fisica-matematica/
[12] https://www.tomshw.it/scienze/un-oggetto-quantistico-e-stato-creato-per-la-prima-volta-in-laboratorio/
[13] Le tri topologique est un terme issu de la géométrie, c’est-à-dire de la théorie des graphes, qui cherche à définir des systèmes qui manifestement ne le sont pas – il cherche ainsi à reconnaître le comportement possible de certaines matières qui manifestement n’ont rien à voir les unes avec les autres et semblent au contraire interagir de manière synchrone. Dans notre cas, la prédictibilité du résultat 1 + 1 dans la dimension quantique est assurée par la localisation dans le champ tridimensionnel de toutes les positions occupées par 1 + 1 – httpshttps://en.wikipedia.org/wiki/Topological_sortingen.wikipedia.org/wiki/Topological_sorting ; https://en.wikipedia.org/wiki/Graph_theory.
[14] https://www.focus.it/scienza/scienze/entanglement-quantistico-intervista-spiegazione
[15] https://arxiv.org/abs/2305.03766
[16] La cohérence quantique repose sur l’idée que tous les objets ont des propriétés ondulatoires. Elle est à bien des égards similaire au concept d’intrication quantique, qui implique des états communs à deux particules quantiques au lieu de deux ondes quantiques d’une même particule. Si les propriétés ondulatoires de différentes particules ou quasi-particules sont identiques (et donc superposées), on parle de cohérence quantique. httpshttps://it.theastrologypage.com/quantum-coherenceit.theastrologypage.com/quantum-coherence .
[17] Il s’agit d’un concept difficile à saisir, lié à une erreur humaine de perception de la réalité. Je m’explique : si un homme souffre de la soif dans le désert, il rêve désespérément de trouver de l’eau. S’il la trouve et qu’il doit boire pour étancher sa soif, il risque de mourir, car il a confondu une de ses projections de la réalité (le besoin d’eau) avec la dépendance quantique (le corps a besoin de l’équilibre entre l’eau et la matière corporelle, et si cet équilibre est rompu, il doit être rétabli dans le corps, en commençant par la peau, et non dans l’estomac, qui a besoin de trop de temps pour transformer l’eau qu’il boit en l’eau dont il a besoin…). httpshttps://lifeshifting.it/2018/05/11/2223/lifeshifting.it/2018/05/11/2223/ ; https://tech.everyeye.it/notizie/numeri-immaginari-indispensabili-descrivere-realta-561343.html ; httpshttps://www.sciencedirect.com/science/article/pii/S0550321322000426www.sciencedirect.com/science/article/pii/S0550321322000426 ; https://www.nature.com/articles/s41535-023-00540-3) .
[18] https://www.europeantimes.news/ru/2023/04/physicists-take-a-step-toward-fault-tolerant-quantum-computing/
[19] https://2051.vision/2023/04/08/chto-takoe-kvantovyy-kompyuter-i-kak-on-rabotaet/
[20] Comme nous l’avons expliqué, même l’addition la plus simple (1+1) donne un seul résultat dans le monde bidimensionnel de l’arithmétique, alors que dans le monde quantique, qui est tridimensionnel, 1+1 peut donner de nombreux résultats, et les qubits sont les unités par lesquelles nous mesurons le nombre énorme de résultats possibles que même l’addition arithmétique la plus simple donne dans le monde quantique. httpshttps://en.wikipedia.org/wiki/Qubiten.wikipedia.org/wiki/Qubit .
[21] https://2051.vision/2023/04/08/chto-takoe-kvantovyy-kompyuter-i-kak-on-rabotaet/
[22] https://habr.com/ru/companies/bigdataplatform/articles/681332/
[23] https://www.corriere.it/scuola/universita/test-ammissione-preparazione-e-orientamento/cards/sono-17-equazioni-che-hanno-cambiato-mondo-quante-ne-sapete/equazione-schroedinger.shtml
[24] https://habr.com/ru/companies/bigdataplatform/articles/681332/
[25] https://habr.com/ru/companies/bigdataplatform/articles/681332/
[26] https://vc.ru/future/548157-kvantovyy-kompyuter-chto-zachem-kogda
[27] https://phys.org/news/2023-05-google-quantum-ai-braids-non-abelian.html
[28] https://www.youtube.com/watch?v=O5Kv3j06oF8
[29] https://phys.org/news/2023-05-nonabelions-quantum-prone-errors.amp
[30] https://cordis.europa.eu/article/id/153918-homotopy-theory-of-higher-categories/it
[31] https://www.google.com/search?client=firefox-b-d&q=kagome+états+excités#ip=1
[32] https://www.chimica-online.it/download/stato-eccitato.htm
[33] https://phys.org/news/2023-05-nonabelions-quantum-prone-errors.html
[34] https://www.zerounoweb.it/analytics/cognitive-computing/quantum-error-scoperte-nuove-particelle-che-danno-speranza/ ; https://www.cmic.polimi.it/magazine/molecular-sciences/nodo-borromeo-supramolecolare-studio-pubblicato-su-chem/ ; https://www.lescienze.it/news/2023/05/16/news/anyoni_nonabelioni_calcolo_qubit_topologici_resistenza_errori-12092348/
[35] https://www.nature.com/articles/d41586-023-01574-0
[36] https://www.nature.com/articles/d41586-023-01574-0
[37] https://arxiv.org/pdf/2305.03766.pdf
[38] http://pages.di.unipi.it/mastroeni/mod/Modelli_su_grafi1.pdf
[39] Il s’agit d’un concept complexe : les équations différentielles tentent d’estimer la valeur d’une quantité initialement inconnue, par exemple x et y. Il s’agit d’un principe simple qui, lorsqu’il est appliqué, devient de plus en plus complexe. Il arrive qu’en démêlant une équation très complexe, on se rende compte qu’il y a des parties de l’équation qui se chevauchent graphiquement et qui sont donc appelées défauts topologiques et qui peuvent être « simplifiées » deux à deux, avec une forte réduction de la complexité globale. C’est encore plus vrai dans le domaine quantique, où les équations sont tridimensionnelles – https://reccom.org/difetto-topologico-rottura-spontanea-della-simmetria/ .
[40] https://nplus1.ru/news/2023/05/16/non-abelian-anyons
[41] En d’autres termes, les non-abelions contribuent à la simplification du calcul quantique et donc à la représentation de calculs complexes, qui sont plus faciles à résoudre grâce à leur existence.
[42] La théorie de la relativité générale, créée par Newton et affinée par Einstein, utilise des calculs bidimensionnels et résout les problèmes posés par le concept de courbure de l’espace. Aujourd’hui, la physique quantique tente de développer une théorie de la gravité qui tienne compte de tout ce que nous avons appris de la physique quantique. Le développement le plus célèbre de cette recherche est la « théorie des cordes », qui suggère que certains qubits peuvent être représentés, en raison de leur mouvement, non pas comme des points, mais comme des cordes. – httpshttps://www.treccani.it/enciclopedia/gravita-quantistica_%28XXI-Secolo%29/www.treccani.it/enciclopedia/gravita-quantistica_%28XXI-Secolo%29/ ; https://plato.stanford.edu/entries/quantum-gravity/ ; https://www.treccani.it/enciclopedia/gravita-quantistica_%28Lessico-del-XXI-Secolo%29/ ; https://plato.stanford.edu/entries/qm-relational/
[43] https://arxiv.org/pdf/2305.03766.pdf
[44] https://nplus1.ru/news/2023/05/16/non-abelian-anyons
[45] Au cours de milliers d’expériences menées dans le monde entier pour améliorer la théorie quantique, les scientifiques ont réalisé qu’il existe des moments où naissent puis meurent des structures cristallines très raffinées, dont la désintégration est due au fait que les particules qui les composent sont éphémères (c’est-à-dire qu’elles n’existent que pendant quelques secondes et se transforment ensuite). Ces particules sont appelées « excitons » et l’analyse de leur phénoménologie s’appelle l’étude des « états exotiques » de la matière – https://it.dayfr.com/tecnologia/436185.html ; https://www.wired.it/scienza/lab/2016/10/04/materia-esotica-nobel-fisica/ ; https://reccom.org/scoperto-un-nuovo-stato-esotico-della-materia/ .
Laisser un commentaire